|
il Solitario del 35
Il Gioco del 35 è un solitario che si può fare ovunque con carta e penna: basta inserire tutti i numeri da 1 a 35 nella tabella, seguendo alcune semplici regole di
percorso:
-
Si parte dalla casella
centrale con il numero 1 (come variante si può partire da una casella
qualsiasi).
-
Si inseriscono i numeri interi successivi, saltando una casella in diagonale e due caselle in
orizzontale e verticale (la lunghezza del salto è quasi uguale).
-
Se il percorso si blocca prima del 35, il gioco non è riuscito: prendiamo un altro foglio di
carta.

Struttura dati
Il campo di gioco dovrebbe essere allocato in una matrice intera
Campo[5][7], dove ogni casella vale o se vuota, da 1 a 35 se occupata.
Occorre però fare qualche considerazione preliminare:
-
In memoria non esistono matrici: il programma alloca un array di 35
elementi.
-
La gestione della matrice con due indici [i] e [j] richiede che, ad
ogni utilizzo di una casella, venga eseguita l'operazione k=i*5+j per
calcolare l'indice sull'array allocato in memoria (operazione inserita
automaticamente dal compilatore).
-
L'esame di una mossa dalla casella [i1][ j1]
alla [i2][ j2] richiede la verifica che gli
indici di destinazione cadano nel campo da gioco:
se (i2>=0 and i2<=5 and j2>=0 and
j2<=7 and Campo[i2][j2]==0) prova mossa
Le operazioni sono decisamente più veloci se utilizziamo come campo di
gioco direttamente un array monodimensionale e inseriamo intorno al campo
5x7 una cornice spessa tre caselle, contenenti tutte il valore fittizio -1: in questo modo
utilizzeremo un solo indice per gli spostamenti, a partire dalla casella
[71], e la verifica di una mossa dalla casella [k1] alla [k2]
diventa :
se (Campo[k2]==0) prova mossa

| int Campo[143]
|
Campo da gioco: ogni casella vale 0 se vuota, da 1
a 35 se occupata, -1 se appartenente alla cornice di protezione. |
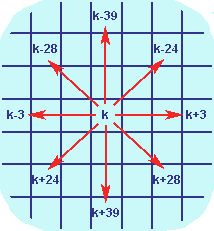
| int Mosse[8] |
Valori degli 8 possibili spostamenti
da una casella alla successiva:
{-39, -28,
-24, -3, +3, +24, +28, +39 } |
| int k |
indice di posizione sul campo da gioco: parte da 71
e si sposta sulle caselle della zona centrale. |
| int Num |
Numerazione progressiva inserita sul Campo: varia
da 1 a 35 |
| int Soluzioni |
Riporta il numero totale delle soluzioni diverse
trovate. |
Algoritmo
Il programma è costituito essenzialmente da una
funzione ricorsiva che, data una situazione sul tavolo di gioco, elenca
tutte le mosse possibili e le prova ad una ad una chiamando
successivamente la funzione stessa per un'ulteriore valutazione.
La ricorsione termina quando si raggiunge il 35 o quando non vi sono mosse
possibili
Il programma termina quando sono state esaminate tutte le mosse successive
al numero 1.
Codice Sorgente in C
Per la codifica è stato usato il linguaggio C; la
versione riportata è per Borland C/C++ 3.1, ma è facilmente adattabile
ad un qualsiasi compilatore C.
Potete scaricare direttamente l'eseguibile (di
soli 9 Kb) per Dos/Windows.
Potete scaricare anche l'APK per Android (di circa 800KB) gratuito e SENZA pubblicità.
Considerazioni finali
Il programma, su un Athlon XP 2600, trova in 18
secondi 13272 soluzioni differenti
(eliminando la visualizzazione delle soluzioni durante il calcolo,
impiegherebbe meno).
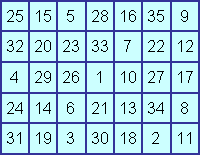
Inserendo il numero 1 in una qualsiasi delle 35
caselle, si perviene comunque a migliaia di soluzioni diverse. Ad esempio,
partendo da una delle quattro caselle di angolo, si trovano 52730
soluzioni.
|




